space-by-time
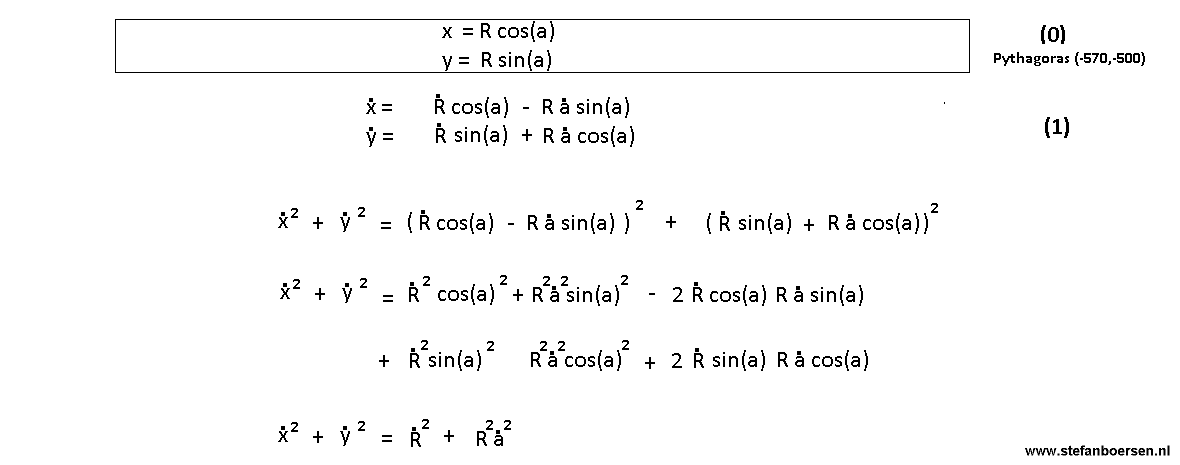
The first order space by time relation

The second order space by time relation
Gustave-Gaspard Coriolis 1792-1843 1
Gustave-Gaspard Coriolis 1792-1843 2
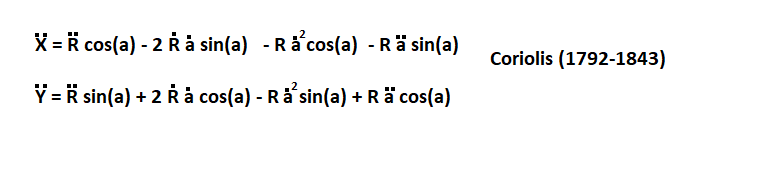
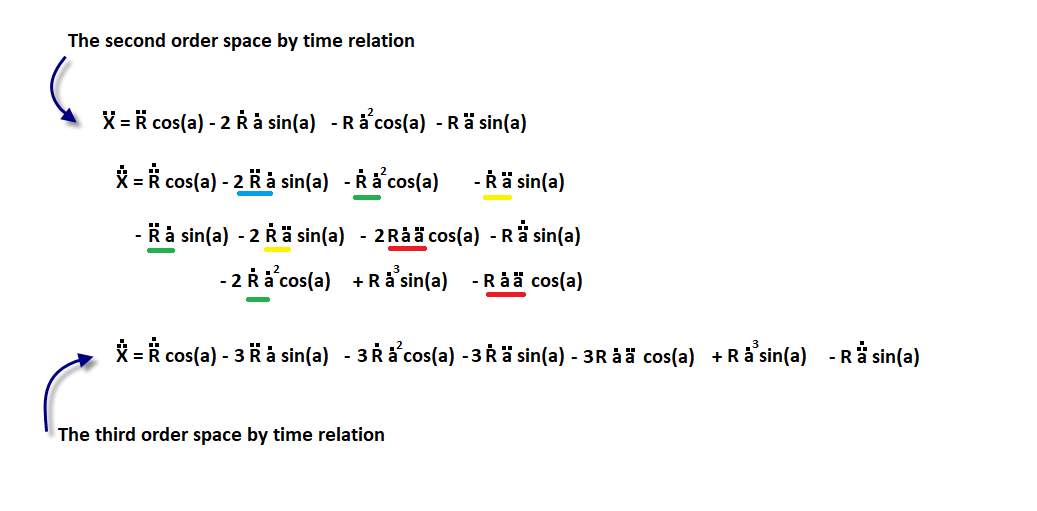
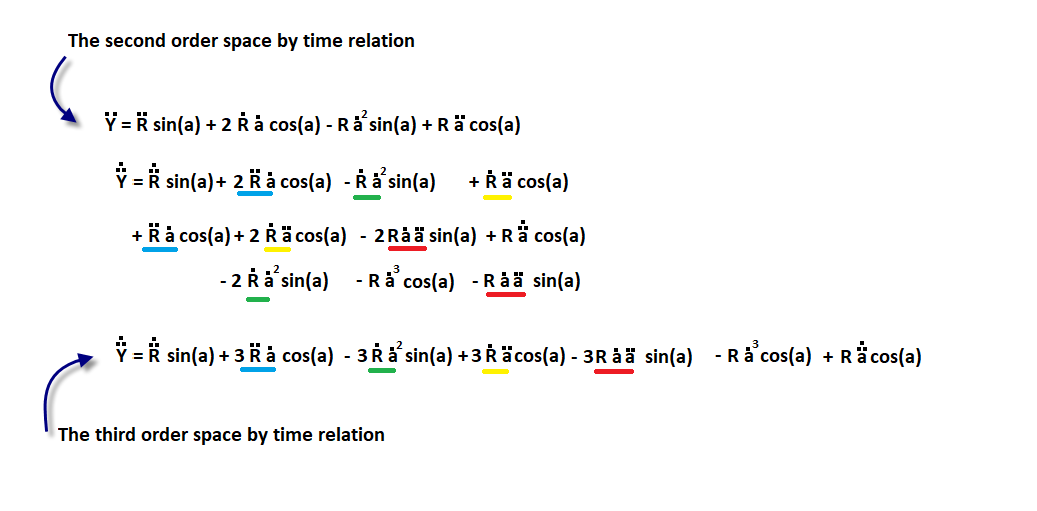



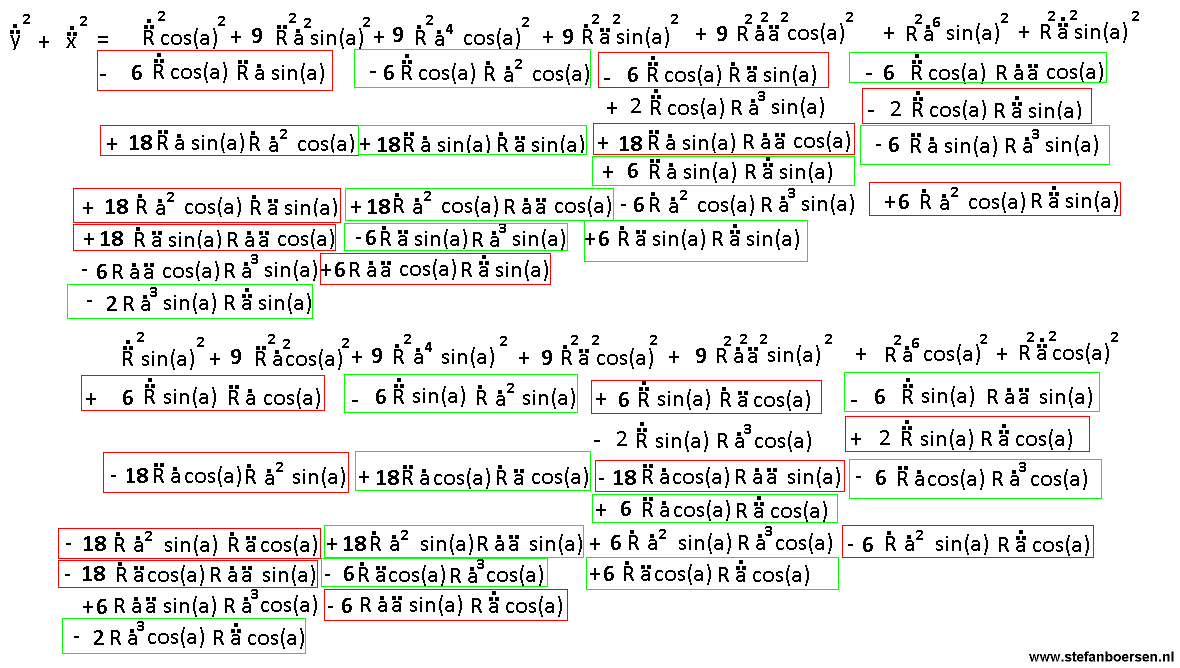
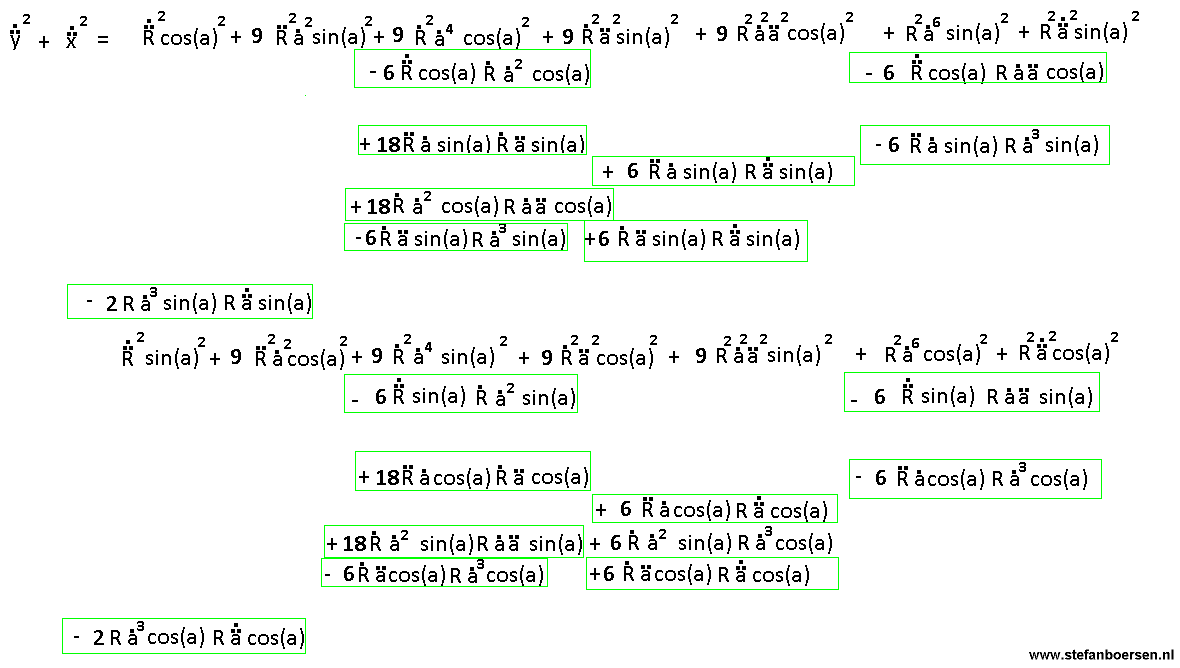
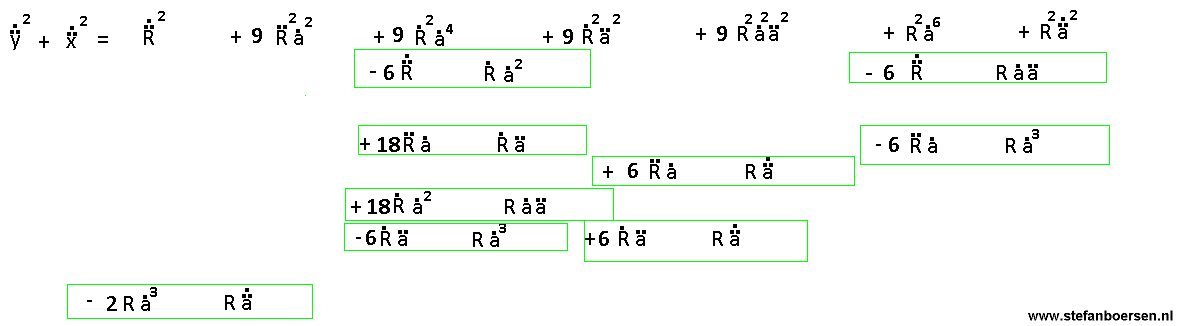
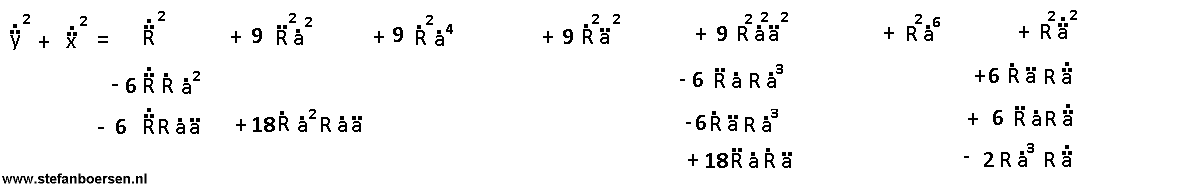
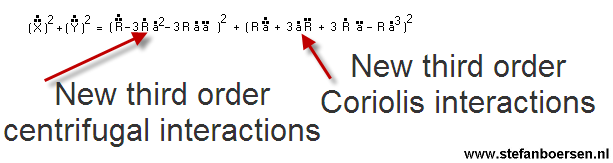
The third order space by time relation
The third order space-by-time relation


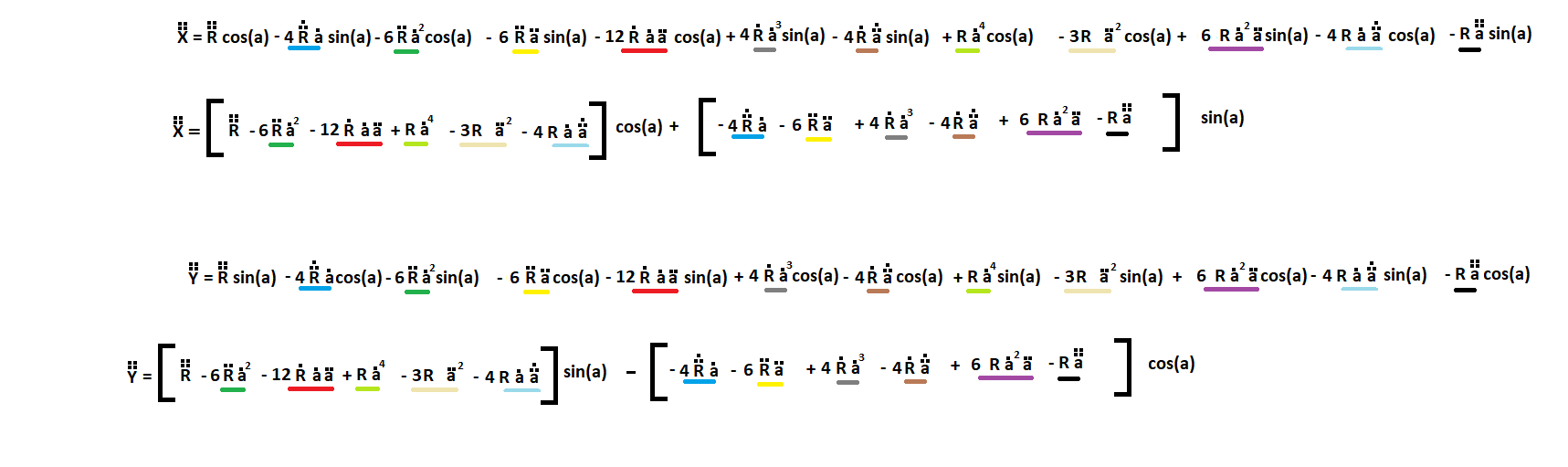
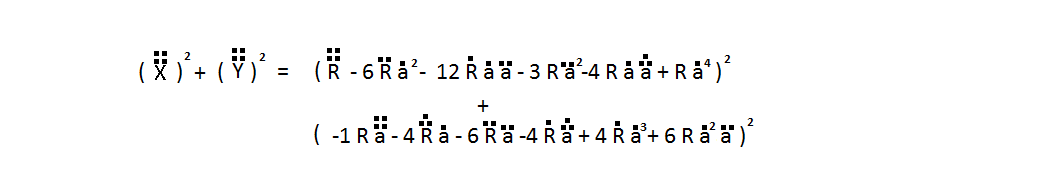
The fourth order space by time relation
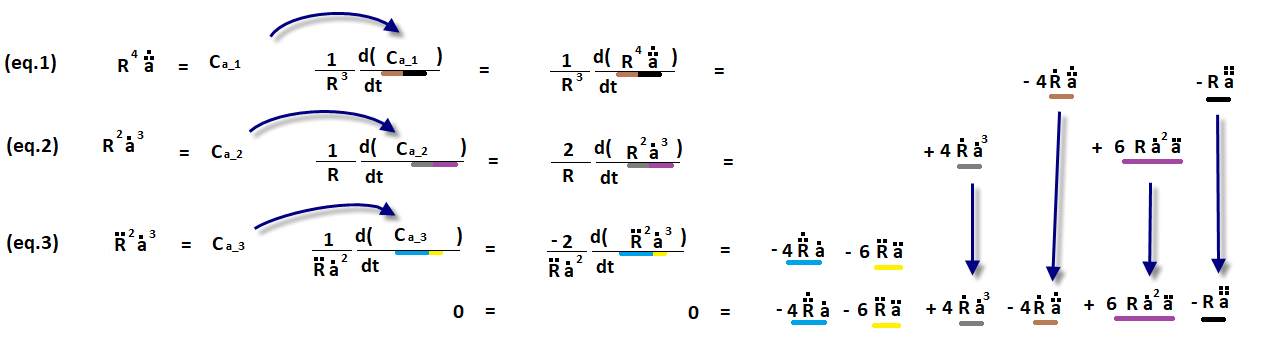
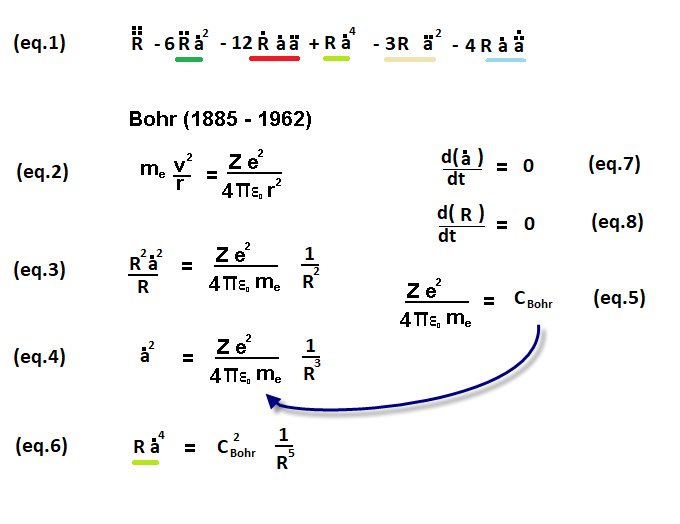
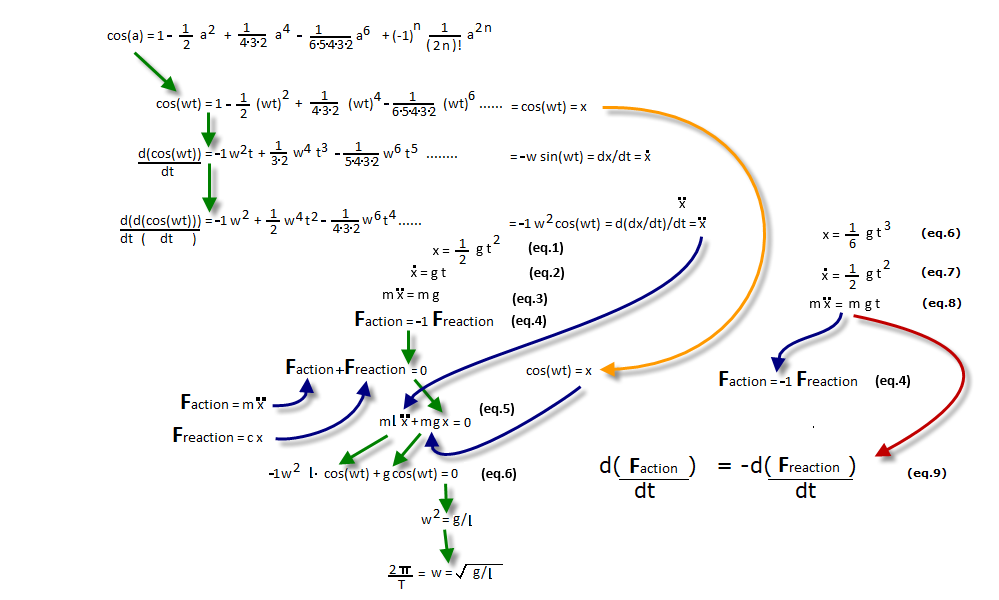
space by time
space-by-time
y\ =\ \sin^2\left(2\cdot\pi\cdot x\right)
y\ =\ \frac{1}{2}-\frac{1}{2}\cos\left(4\cdot\pi\cdot x\right)
y\ =\ \frac{86}{1000}\ \cdot\frac{\left(1+r\right)^x-1}{r}
import sympy as sp
# Symbol for time
t = sp.symbols('t')
# R(t) and a(t) are functions of time
R = sp.Function('R')(t)
a = sp.Function('a')(t)
# Define x(t) and y(t)
x = R * sp.cos(a)
y = R * sp.sin(a)
# Compute 4th derivatives
x_4 = sp.diff(x, t, 4)
y_4 = sp.diff(y, t, 4)
# Magnitude squared of the 4th derivative vector
fourth_order_magnitude_squared = sp.simplify(x_4**2 + y_4**2)
# Pretty print the result
sp.pprint(fourth_order_magnitude_squared)
\[
(\dddot{X})^2 + (\dddot{Y})^2 =
\left( \dddot{R} - 6\dot{R} \dot{a}^2 - 12 \dot{R} a \ddot{a} - 3 R \dot{a}^2 \ddot{a} - 4 R \dot{a} \dddot{a} + R \dot{a}^4 \right)^2
+
\left( - R \dot{a} \ddot{a} - 4 \dot{R} \dot{a} a - 6 R \dot{a} \ddot{a} + 4 R \dot{a}^3 + 6 R \ddot{a}^2 \right)^2
\]
\[
\left( \ddddot{x} \right)^2 + \left( \ddddot{y} \right)^2 =
\left( \frac{d^4}{dt^4} \left[R \cos(a) \right] \right)^2 +
\left( \frac{d^4}{dt^4} \left[R \sin(a) \right] \right)^2
\]