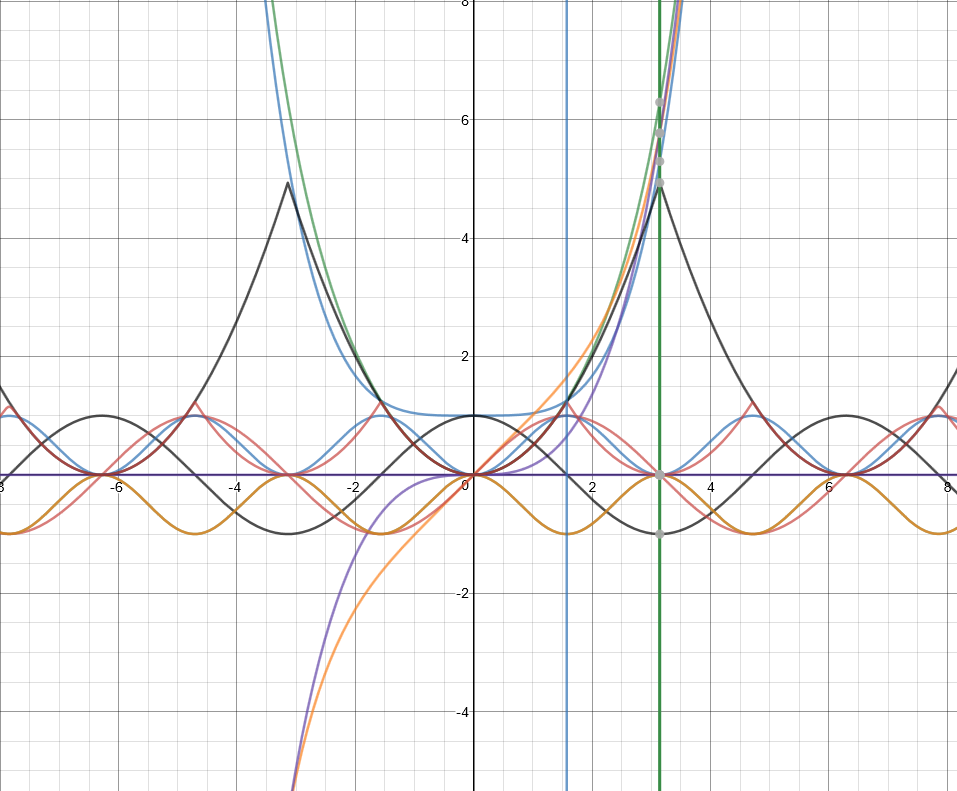
f\left(x\right)=1+\frac{x^4}{4!}\ +\ \frac{x^8}{8!}\ +\ \frac{x^{12}}{12!}+\frac{x^{16}}{16!}+\frac{x^{20}}{20!}

g\left(x\right)=\frac{x^2}{2!}\ +\ \frac{x^6}{6!}+\frac{x^{10}}{10!}+\frac{x^{14}}{14!}+\frac{x^{18}}{18!}+\frac{x^{22}}{22!}

h\left(x\right)=\frac{x^1}{1}\ +\ \frac{x^5}{5!}+\frac{x^9}{9!}+\frac{x^{13}}{13!}+\frac{x^{17}}{17!}+\frac{x^{21}}{21!}

k\left(x\right)=\frac{x^3}{3!}\ +\ \frac{x^7}{7!}+\frac{x^{11}}{11!}+\frac{x^{15}}{15!}+\frac{x^{19}}{19!}+\frac{x^{23}}{23!}

l\left(x\right)=f\left(x\right)-g\left(x\right)

m\left(x\right)=h\left(x\right)-k\left(x\right)

n\left(x\right)=\ m\left(x\right)\cdot m\left(x\right)

o\left(x\right)=\left(\left(k\left(x\right)-h\left(x\right)\right)\cdot\left(h\left(x\right)-k\left(x\right)\ \ \right)\right)

q\left(x\right)=-1\cdot\left(h\left(x\right)\cdot h\left(x\right)+k\left(x\right)\cdot k\left(x\right)\ -2\cdot h\left(x\right)\ \cdot k\left(x\right)\right)

p\left(x\right)\ =\ o\left(x\right)+n\left(x\right)

y=\ \frac{1}{2}\cdot\arccos\left(\cos\left(x\right)\ \right)\ \arccos\left(\cos\left(x\right)\ \right)

r\left(x\right)=-\frac{1}{2}\left(\arcsin\left(k\left(x\right)-h\left(x\right)\right)\cdot\arcsin\left(h\left(x\right)-k\left(x\right)\ \ \right)\right)

x=\frac{\pi}{2}

x\ =\ \pi